THEME: Vers la preuve
France  -  Quatrième  -  Maths

But: Somme de trois nombres consécutifs

Pour faire travailler les élèves sur les preuves en algèbre, nous proposons aussi des preuves portant sur des propriétés arithmétiques. Cela nous permet de travailler sur l’expression algébrique de deux nombres entiers consécutifs, de nombres pairs ou impairs, de multiples de …, etc. Cette activité peut être proposée dès la classe de 5ème.

Mise en oeuvre: Somme de trois nombres consécutifs

Sur un temps de mise en train

Cette activité est mise en œuvre avec les objectifs suivants :

- mettre en valeur une démarche de recherche : essais, conjecture, preuve,

- montrer l'intérêt des propriétés algébriques (distributivité simple, double distributivité, commutativité...) dans le mécanisme de preuve,

- convaincre de la nécessité du passage au calcul littéral pour prouver une affirmation sur une infinité de valeurs,

- mettre en place des stratégies de modélisation algébrique de problèmes arithmétiques,

- revenir sur l'écriture des nombres consécutifs, des multiples

Synthèse: Somme de trois nombres consécutifs

En plus de la propriété arithmétique découverte et prouvée, la somme de trois nombres consécutifs est un multiple de trois, l'institutionnalisation peut mettre en avant :

- on ne prouve pas la conjecture avec des exemples, il faut utiliser des lettres et des propriétés.

- la preuve peut être plus facile ou plus difficile suivant le choix de l'écriture des nombres consécutifs.

Réactions d'élèves: Somme de trois nombres consécutifs

Voici quelques copies d'élèves de début de quatrième :

Dans cette première copie, des essais, pas de conjecture écrite, mais on voit en rouge la réflexion de l'élève.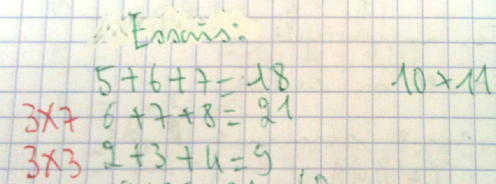

Pour cet autre élève après les essais on voit qu'il écrit plusieurs conjectures, il cherche à mettre en avant des propriétés arithmétiques

La conjecture est donnée en langage naturel

Avec le passage à la lettre

Prolongement: Somme de trois nombres consécutifs

Autre présentation possible de cette activité :

qui peut-être prolongée par la question suivante :

Dans certaines classes, des élèves souhaiterons prolonger la recherche et chercherons une généralisation, ça peut-faire l'objet d'un devoir à la maison ou d'une recherche longue avec des temps de mise en commun une fois par semaine.

D'autres preuves portant sur des propriétés arithmétiques :

en 5ème :

à partir de la 4ème après la mise en place de la double distributivité :