THEME: 12 - Les pyramides
Ressource 3: La pyramide pour raisonner
1 Celle du site :
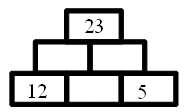
Cette pyramide est différente. Pour essayer de compléter la pyramide, il va falloir répartir le nombre du sommet dans les cases qui le soutiennent. Cette fois il y a un choix à faire. Ils vont faire des essais et corriger leurs propositions en fonction de l'écart trouvé entre le sommet dépendant du nombre choisi et le sommet demandé.
Des procédures vont apparaître : l'écart entre 16 et 23 est 8 donc le nombre qui manque à la base est 4 (8:2). Il est intéressant que les élèves les mutualisent.
Ce sont ces pyramides que l'on utilise en 4eme comme préparation au chapitre des équations. On peut envisager de travailler les pyramides de niveau 3 dès la 5ème.
2 Celles dont on connait les nombres de la base
Comme décrite dans le bulletin vert (n°491)
Dans une pyramide à quatre étages, comment placer sur la ligne inférieure quatre nombres donnés, pour obtenir le plus grand nombre possible au sommet ?
Les élèves se rendent compte qu'il y a une symétrie dans le placement des nombres et que les places du milieu ont plus de poids que celles des bords.
Avec le travail de simplification d'écritures de 5eme, on peut trouver pour le nombre du sommet : a+3b+3c+d
Ce type de recherche peut aussi se faire avec des nombres relatifs à la base.
Ou une variante : connaissant les nombres de la base, quelles peuvent être les valeurs au sommet ?
Ou une autre : connaissant les nombres de la base, peut-on avoir 25 au sommet ?
3 Celles dont on connaît le nombre au sommet
Encore dans le bulletin vert (n°491)
Quel nombre identique faut-il placer dans chacune des quatre cases de la base de la pyramide pour obtenir 136 au sommet.
Pour les élèves qui trouvent rapidement, on rajoute un autre nombre au sommet toujours multiple de 8, puis un qui ne l'est pas → ici encore on peut dès la 5eme et avec la simplification d'écriture montrer que le nombre au sommet est du type 8a
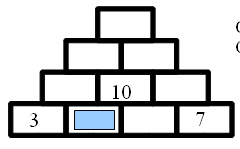
4 Celles dont le nombre au sommet est indépendant du choix initial (encore BV)
Compléter en prenant 8 pour la case en bleu. Recommencer en prenant 18. Qu'en pensez vous ? → la confirmation sans l'algèbre est impossible.