THEME: 11 - Les programmes de calcul
Ressource 4: Les programmes de calculs pour résoudre des équations
Par exemple avec ce programme de calcul :
Je
choisis un nombre.
Je le multiplie par 3.
J’ajoute 5 au résultat.
Quel est le résultat final si j’ai choisi 8 ?
Quel nombre est choisi si j’obtiens 17 ?
La première fois que l'activité est proposée, les élèves font des essais-erreur ou modélisent le problème (le plus souvent dans leur tête) par une opération à trou. Lors de la mise en commun, les élèves débattent sur les opérations réciproques et sur l'importance de l'ordre dans lequel on les effectue. Nous mettons donc en place une technique qui est justifiée par les opérations « réciproques » même si on reste dans le cadre des nombres positifs.
Après quelques exercices semblables, des élèves introduisent les ostensifs suivants qui sont ensuite majoritairement adoptés par la classe et qui constituent un outil local et transitoire de résolution des problèmes de ce type :
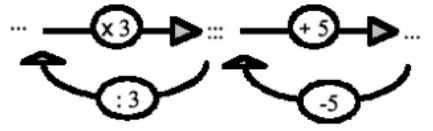
Nous introduisons aussi le quotient dans ce même esprit en proposant par exemple 6 comme nombre final dans le programme ci-dessus. Ceci permet de créer des liens entre les notions.
En classe de cinquième, nous présentons souvent le programme sous la forme d'une phrase dictée à l'oral en langue naturelle. Les élèves ont à prendre en note les informations nécessaires. Cela les incite à simplifier leur écriture jusqu'à remplacer le nombre cherché par un symbole ou, en fin d'année, par une lettre. Voici la production d’un élève de 5ème sur le problème suivant (on peut voir l’utilisation des flèches) :

Cet élève commence par faire deux essais (1 et 2 sont les premiers nombres auxquels les élèves pensent en général quand on débute ce genre d'activité). L'élève remarque alors que le résultat 18 se trouve entre 16 et 22 et donc réalise des essais avec des nombres décimaux compris entre 1 et 2. Le programme de calcul est symbolisé à l'aide de flèches. Après plusieurs essais (1,4 donne 18,4), l'élève « remonte » le calcul. On voit ici toute l’importance des variables didactiques car c’est bien la valeur choisie (nombre rationnel) qui oblige l'élève à avoir recours à cette méthode
Ce travail est poursuivi en faisant évoluer la technique en amenant les élèves à traduire le programme à l'aide d'une seule expression numérique pour qu’ils visualisent dans l'expression les constantes et les variables. En effet, en cinquième, débute aussi l'écriture des programmes de calcul à l'aide d'une expression littérale. L’utilité de cette écriture peut prendre du sens pour les élèves dans le cas où le programme ne peut pas être remonté. Il est alors utile de modifier l'expression en utilisant la distributivité pour obtenir une expression qui corresponde à un programme équivalent qui lui, peut être remonté. Les élèves n'ont pas recours à la résolution experte d'équations. On voit ici l’importance donnée à la propriété de distributivité qui a été travaillée par ailleurs.
L'exemple suivant montre le type de problème posé en fin de 5ème (ou début de 4ème).
Je choisis un nombre
Je lui ajoute 3
Je multiplie le résultat par 5
je soustrais le nombre choisi
Quel nombre ai-je choisi si j'obtiens 35, si j'obtiens 25, si j'obtiens 28 ?
Notons que le fait de soustraire le nombre choisi pose problème à de nombreux élèves qui oublient cette partie du calcul ou soustraient x+3
Lors de la mise en commun, les élèves mettent en avant la différence entre ce programme et les précédents. Cet échange aboutit à un bilan intermédiaire : « on ne peut pas remonter ce programme car on soustrait le nombre à la dernière étape ».
Certains élèves vont introduire une expression littérale pour simplifier le programme de calcul comme en témoigne cette production d'élève qui tout d’abord symbolise le programme de calcul à l'aide de flèches, mais la dernière flèche est « vide » (-... pour symboliser que l'on retranche le nombre choisi).

Une tentative de remontée est rayée puis l'élève a recours à une expression littérale pour écrire le programme de calcul : il désigne par x le nombre choisi et utilise les propriétés d'algèbre pour simplifier le programme. Un retour au symbolisme avec les flèches permet ensuite de faire apparaître le programme simplifié qui est équivalent au précédent (prouvé). Il est ensuite possible de le remonter . Une vérification avec le programme de l'énoncé est ensuite faite.
Nous proposons alors l’institutionnalisation suivante : « un programme de ce type peut être simplifié en utilisant les propriétés d'algèbre. L'expression obtenue correspond à un programme de calcul qui peut être remonté ».
Les élèves gardent le lien entre l'écriture littérale et la présentation sous forme de programme de calcul. Il ne s'agit pas ici de résolution experte d'équations.
Lorsque l'on propose à nouveau ce type de programme de calcul, nous modifions les variables didactiques pour que les nombres cherchés soient difficilement accessibles par essais-erreur, ce qui oblige à utiliser les expressions littérales.
En classe de 4ème, notons que comme les élèves sont familiarisés avec ce type de présentation des problèmes, ils cherchent volontiers. Nous proposons alors des programmes de calculs agissant sur l'inconnue dans les deux membres.
Dans un premier temps, nous choisissons des programmes qui ont des solutions entières simples, les élèves cherchent la solution par tâtonnement. Ils s'enrichissent des stratégies de leurs pairs, ce qui conduit à des essais plus organisés (dichotomie, utilisation de la linéarité).
Nous jouons ensuite sur les variables didactiques pour décourager le tâtonnement (solutions négatives, décimales, rationnelles). Les élèves se rendent bien compte que le problème vient de la présence du nombre à chercher dans les deux membres et ils essaient de l'éliminer. L'objectif est de les amener intuitivement vers les règles d'opérations sur les égalités en passant par une représentation, l'utilisation d'un symbole à la place de la lettre (image mentale de la balance). En augmentant le coefficient de x ou en proposant un coefficient négatif, on oblige les élèves à s'extraire du dessin.
Nous continuons avec des problèmes ayant les mêmes solutions pour permettre aux élèves de comprendre les règles d'opérations sur les égalités. Durant ce travail, qui est très en amont du chapitre sur les équations, aucune formalisation n'est exigée. La question de la validité des règles utilisées nécessite qu'elles soient prouvées et institutionnalisées dans une leçon « Ordre et opération » distincte de la leçon sur les équations.
Voici quelques travaux d'élèves de 4ème qui nous permettent de montrer des stratégies différentes sur le problème suivant donné oralement :
Je cherche un nombre tel que si je le multiplie par 3 et que j'ajoute 8,
je trouve le même résultat que si je le multiplie par 7 et que j'ajoute 5.
- essais/erreur, de plus en plus organisés, utilisant l'écart entre les résultats des deux programmes ;
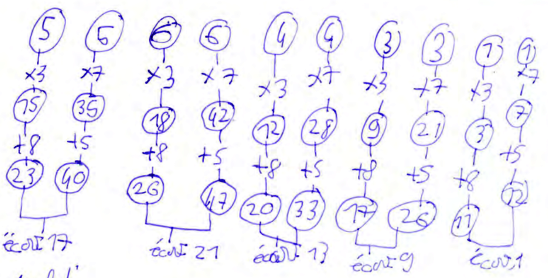
ou un travail sur les écarts entre les termes avec l'inconnue et les nombres dans chaque membre avec une vérification et des essais sur le signe et les nombres à diviser. Un travail sur les écarts entre les termes avec l'inconnue et les nombres dans chaque membre avec une vérification et des essais sur le signe et les nombres à diviser.
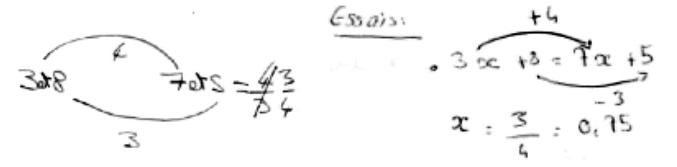
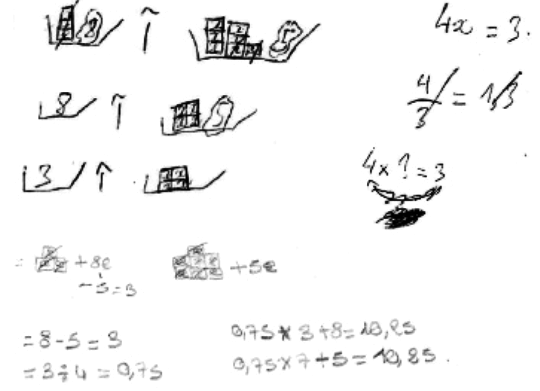
- schématisation avec l'image de la balance (qui n'est possible que lorsque les nombres sont bien choisis) ;
- passage aux expressions littérales et utilisation des théorèmes d'algèbre.
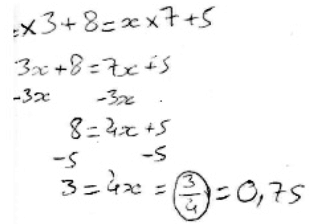
Nous avons donné rapidement une organisation mathématique possible, utilisant les programmes de calcul, permettant de travailler les équations tout au long du collège. Comme nous l’avons dit, d’autres problèmes sont proposés qui nécessitent aussi d’avoir recours aux équations. Les programmes de calcul pourront être utilisés à cette occasion car il est également possible de « retraduire » des équations sous forme de programmes pour aider à la résolution et de façon plus générale, à développer des liens entre les différents types de tâches, voire les techniques.
Nous utilisons de nombreux programmes en mise en train, ce qui permet de travailler l’algèbre en continu et pas seulement lors du ou des chapitres dévolus. Nous pensons que cet apprentissage est complexe et nécessite du temps.