THEME: Vers les équations
France - (pas de niveau associé) ((pas de niveau associé)) - Maths
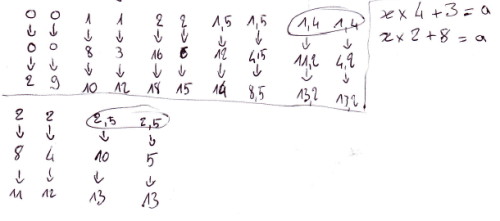
Activité 4: Programmes que l'on ne peut pas remonter

Réactions d'élèves: Programmes que l'on ne peut pas remonter
Voici quelques copies d'élèves : Jeanne cherche la solution par tâtonnement, ses essais sont organisés et comme la solution est simple, elle la trouve rapidement. Il faudra par la suite jouer sur les variables didactiques pour décourager le tâtonnement (solutions négatives, décimales, rationnelles).