THEME: Vers les équations
France - (pas de niveau associé) ((pas de niveau associé)) - Maths
Activité 3: Deux triangles, leurs aires...
Adaptation de l'exercice 75 p.136 du livre de 4ème Triangle (Hatier 2002)
E est un point du segment [AB]
(CB) est perpendiculaire à [AB] et BC = 5,6 cm
(DA) est perpendiculaire à (BA) et DA = 2,4 cm
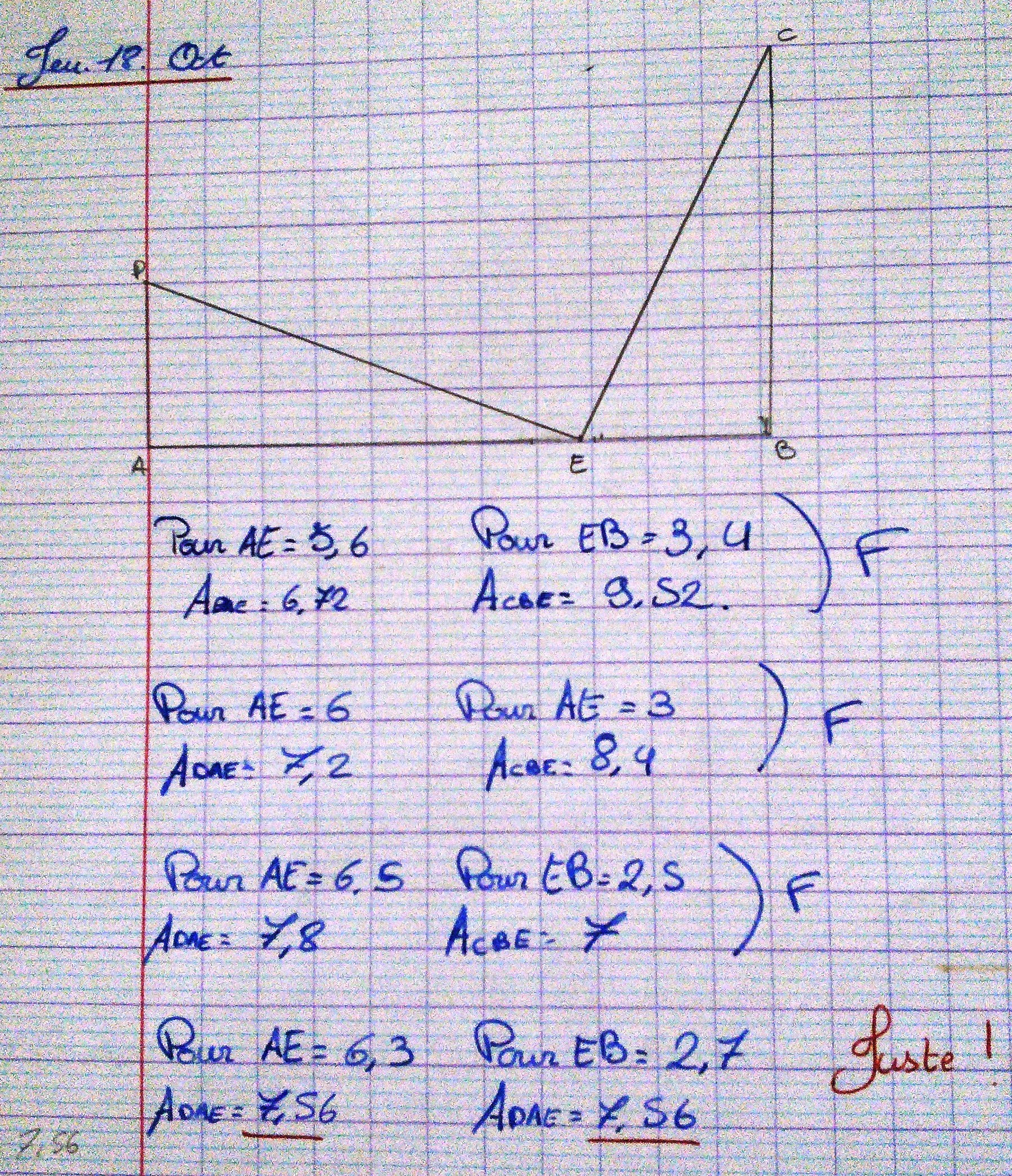
Lorsque [AB] mesure 9 cm, où faut il placer le point E pour que l'aire du triangle BCE soit égale à l'aire du triangle ADE ?
Mise en oeuvre: Deux triangles, leurs aires...
Les problèmes de points mobiles peuvent se résoudre en changeant de cadre. Il faut traduire la dépendance entre les deux variables.
L'élève a à sa charge le fait de choisir BE = x
et surtout EA = 9 - x pour écrire l'équation visée (bien sur le choix peut aussi être EA = x) :
5,6 x = 2,4 ( 9 - x )
Cet apprentissage : choix de x, en déduire 9-x ne peut se faire que si l'élève en éprouve vraiment le besoin parce que la résolution du problème le nécessite et non parce que le professeur l'exige.
Penser à 9 - x est encore plus difficile à faire comprendre que le choix de x. Les élèves proposent souvent 5,6x et 2,4y avec x+y =9, c'est un passage nécessaire qu'il est bon de laisser s'exprimer. Il aide à la compréhension, car dans les premières situations les élèves ne trouvent pas souvent eux-mêmes.
Ce type de problèmes doit donc être proposé en recherche plusieurs fois, en classe et pas forcément à la fin du chapitre. Il peut être intéressant de faire faire des activités de ce type aux élèves dès la classe de 5ème ou le début de 4ème, en choisissant bien les variables didactiques, pour encourager la recherche par essais erreur qui sera mise en défaut ensuite.
Prolongement: Deux triangles, leurs aires...
Toujours avec cette situation et cette figure, nous pouvons proposer des prolongements qui touchent à d'autres parties du programme. Voici quelques propositions :
|
Pour un élève de 4ème ces écritures peuvent constituer une rencontre avec des lettres ayant plutôt le statut d'inconnue pour x et de paramètre pour AB (sans que ce terme soit employé bien sûr), ou bien, on peut aussi y voir aussi la formule BE = (3/4) AB, cette écriture étant souvent utilisée au collège, elle peut être aussi un moyen de passer à la fonction linéaire f(x) = (3/4) x.
Réactions d'élèves: Deux triangles, leurs aires...