THEME: Distributivité et identités remarquables
France - Troisième - Maths
Activité 3: Première Identité Remarquable (ancienne version)
Énoncé du problème
1ère étape :
- au tableau on écrit :
3,2 2,8
10,24 + 7,8418,08 + 2 x 3,2 x 2,8
36
- on choisit deux nombres quelconques
- on calcule, pour chacun, leur carré
- on fait la somme de leurs carrés
- on ajoute au résultat deux fois leur produit
- qu'obtient-on ?
2ième étape :
- on recommence avec 6,1 et 0,9
- on recommence avec 4 et 3
Choisir d'autres exemples
Écrire une conjecture
Démontrer votre conjecture
But: Première Identité Remarquable (ancienne version)
Les activités suivantes servent à introduire les IR. L'objectif est, entre autres :
de présenter et faire fonctionner ces IR dans le sens d'une factorisation (qui seul justifie leur introduction)
d'attirer l'attention de l'élève sur le double-produit (sa construction et son utilité) en partant du fonctionnement naturel des élèves qui consiste à n'écrire que les carrés...
Liens avec les principes
nécessité d'introduction de la lettre
utilisation des propriétés d'algèbre comme outil de preuve
familiarisation de l'élève avec la démarche de recherche
présentation de la première identité remarquable sous la forme "expression développée => expression factorisée
Mise en oeuvre: Première Identité Remarquable (ancienne version)
Durée totale :
40 min
Matériel :
un transparent de consignes à projeter au rétro ou vidéo-projecteur
Déroulement
- 10' (y compris installation de la classe) : l'enseignant présente au tableau les trois ou quatre schéma précédents sans ajouter prématurément de commentaire
- 30 ' : par groupes de deux, on demande aux élèves de répondre aux questions 1,2 et 3 - l'enseignant circule dans la classe - Les élèves répondent sur une feuille que l'enseignant ramasse à la fin de la séance afin de préparer une synthèse pour le cours suivant. On peut aussi envisager une organisation de classe par groupes de 4 (prévoir feutres et transparents dans ce cas)
- fin : une fois la synthèse de ce problème effectuée l'enseignant donne le problème suivant comme exercice de réinvestissement en travail individuel ou à effectuer pour la fois suivante.
Remarque
il peut être difficile pour les élèves de retrouver le carré de la somme des deux nombres proposés. C'est pour cette raison que la troisième étape fait intervenir des nombres relativement simples (4 et 3). C'est aussi pour cette raison qu'il faudra éventuellement faire réaliser plusieurs autres exemples aux élèves. Par contre, comme on souhaite insister sur le rôle du double-produit, on prendra le soin de laisser les élèves deviner d'eux-même que le nombre final est le carré de la somme des deux nombres de départ.
Synthèse: Première Identité Remarquable (ancienne version)
Quels que soient les nombres ou expressions mis à la place de ou de
ou de  on a :
on a :
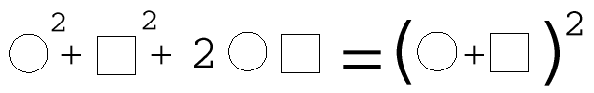
On
dit que le carré d'une somme est la somme des carrés
augmentée du double produit des deux termes.
Dans les
livres on trouve : (a+b)² = a² + 2ab + b²
Preuve : à rédiger avec les élèves
Remarque
: il est important d'insister sur
les quantificateurs et de montrer que la formule constatée est
valable y compris avec des nombres décimaux, négatifs.
Cela peut se faire au cours de la correction et de la synthèse
de l'activité.
Réactions d'élèves: Première Identité Remarquable (ancienne version)
Nous avons noté que les élèves éprouvaient moins de difficultés dans le choix des inconnues que lors des deux premières activités. Dans cette activité, le sens de conjecture et le sens de démonstration sont différents. C'est à souligner lors de la synthèse, comme une technique parmi d'autres pour prouver l'égalité de deux expressions littérales.
A nouveau on notera l'importance des quantificateurs qui sont rappelés dans la synthèse (« quels que soient les nombres ou expressions mis à la place de... ») La présentation de la synthèse fait volontairement intervenir la formulation « naïve » ... et... car cela permet de gérer de manière efficace l'utilisation de parenthèses dans le cas ou ... et ... sont des expressions complexes.
Dans cette activité, le double-produit est volontairement présenté à la suite des deux carrés a² et b². Notre idée est ainsi de s'appuyer sur le fonctionnement naturel des élèves qui consiste a n'écrire que a² et b². Nous proposons ici de faire constater à l'élève que cela ne suffit pas et qu'il faut nécessairement ajouter (ou soustraire) ce double-produit.
Beaucoup d'élèves confondent 2ab et 2a+2b. La structure de ce double-produit semble mettre du temps à s'installer. A la suite de ces activité et des exercices qui les accompagnent, des élèves ont spontanément posé la question de la factorisation des expressions a²+b²+c où c n'est pas le double-produit de a et b. Peut-être l'occasion de prolonger ces activités ?