THEME: Distributivité et identités remarquables
France - Cycle 4 - Maths
Activité 5: Troisième identité remarquable (ancienne version)
a et b sont deux nombres tels que : a + b = 28 et a - b = 6
Trouvez a et b puis calculez a² - b²
Recommencez avec d'autres nombres a et b
Quelle règle trouvez-vous ? Démontrez la
Mise en oeuvre: Troisième identité remarquable (ancienne version)
Fin du travail
d'introduction des identités remarquables.
Cette troisième IR peut éventuellement déjà avoir été évoquée ou utilisée par les élèves.
Durée totale : 1 heure
Matériel : un transparent de consignes à projeter au rétro ou vidéo-projecteur
Déroulement :
10' (y compris installation de la classe) : l'enseignant présente le problème au tableau
30 ' : les élèves travaillent par groupes de 4. Il leur est demandé, de manière beaucoup moins guidée que les fois précédentes, de produire la règle et sa démonstration.
Remarque : pour les groupes qui ont du mal à démarrer, on pourra leur proposer de recommencer avec a=5,9 b=1,1 puis a=10 b=2
Synthèse: Troisième identité remarquable (ancienne version)
Quels que soient les
nombres ou expressions mis à la place de ou de
ou de  on a :
on a :
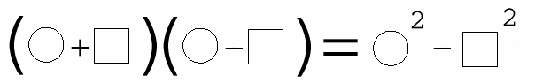
On dit que le produit de
la somme et de la différence de deux nombres est la différence
des carrés de ces deux nombres.
Dans les livres on trouve : (a+b)(a-b) = a² - b²
Preuve : à rédiger avec les élèves