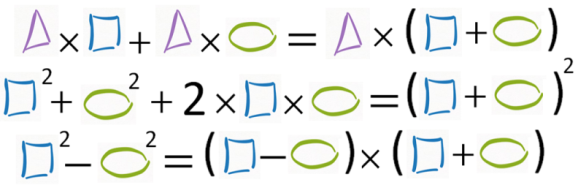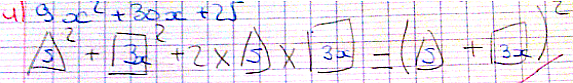4-La factorisation
Activité: Les programmes / nos choix
Programmes de l’enseignement des mathématiques - BO spécial n°6 du 28 août 2008
Avant la troisième, les contenus du programme n'évoquent pas la
factorisation :
En 5ème, dans la sous-partie,
« Distributivité de la
multiplication par rapport à l’addition. », il est
simplement indiqué
« Sur des exemples littéraux, utiliser
les égalités k(a + b) = ka + kb et k(a - b) = ka - kb dans les deux sens. »
Comme en cinquième pour la distributivité, il n'est pas fait référence à la factorisation ou au développement...
Plusieurs remarques pour éclairer nos choix :
Les titres font référence tantôt à une propriété tantôt à une tâche. Nous séparons très clairement les deux dans notre enseignement. Nous explicitons aux élèves que pour traiter une expression littérale (la développer, la factoriser …), il faut utiliser des propriétés (commutativité, distributivité … puis identités remarquables).
Nous utilisons le vocabulaire développement, factorisation dès la 5ème et nous insistons sur la notion de produit et de somme pour préparer le travail par exemple sur les équations produits en 3ème.
Nous présentons les propriétés sous forme de « moules » qui peuvent contenir un nombre, une lettre ou une expression simple.
Pourquoi ne pas parler de factorisation et de développement ? C'est cependant une pratique commune dans les classes.
En 4ème : la partie « calcul littéral » du programme est sous-titrée « développement » et indique : - Réduire une expression littérale à une variable, du type : 3x – (4x – 2); 2x2 – 3x + x2… - Développer une expression de la forme (a + b) (c + d). Dans les commentaires, apparaît de façon anecdotique : Les activités de factorisation se limitent aux cas où le facteur commun est du type a, ax ou x2.Comment les élèves peuvent-ils s'emparer par exemple de 2x2 + 3x2 ? Est-ce une réduction ? Est-ce une factorisation ? Il nous semble qu'il conviendrait de faire référence à la distributivité tant que cette tâche n'est pas automatisée
En 3ème, une des sous-partie du calcul littéral est clairement intitulée « factorisation » et correspond aux contenus suivants : Factoriser des expressions algébriques dans lesquelles le facteur est apparent. La seconde sous-partie « identités remarquables » indique : Connaître les identités : (a + b)(a – b) = a2 – b2 (a + b)2 = a2 + 2ab + b2 (a – b)2 = a2 – 2ab + b2 Les utiliser dans les deux sens sur des exemples numériques ou littéraux simples.Comme en cinquième pour la distributivité, il n'est pas fait référence à la factorisation ou au développement...
Plusieurs remarques pour éclairer nos choix :
Les titres font référence tantôt à une propriété tantôt à une tâche. Nous séparons très clairement les deux dans notre enseignement. Nous explicitons aux élèves que pour traiter une expression littérale (la développer, la factoriser …), il faut utiliser des propriétés (commutativité, distributivité … puis identités remarquables).
Nous utilisons le vocabulaire développement, factorisation dès la 5ème et nous insistons sur la notion de produit et de somme pour préparer le travail par exemple sur les équations produits en 3ème.
Nous présentons les propriétés sous forme de « moules » qui peuvent contenir un nombre, une lettre ou une expression simple.
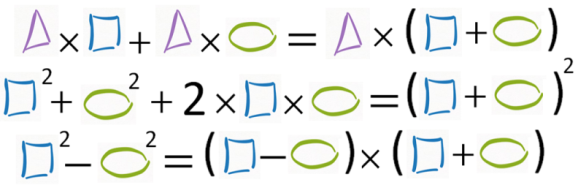
Ce qui peut donner pour les élèves :
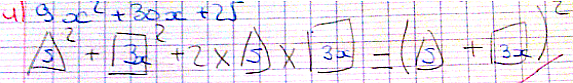
En ce qui concerne les identités remarquables, leur utilisation pour développer vient en complément de la distributivité (simple et double) qui n'est pas toujours très bien maîtrisée en début de 3ème. Nous préférons donc entretenir les automatismes liés à la distributivité avant d'en créer d'autres. Nous laissons donc aux élèves, le choix de leur méthode de développement.
Enfin, nous nous questionnons sur la précocité des travaux de simplification d'écriture des expressions littérales qui rend difficile la reconnaissance des sommes et des produits et qui augmente la confusion entre double et carré.