Énoncé du problème
Niveau(x) concerné(s) : seconde
Adaptation de l'exercice 41 p.144 du livre de seconde Hyperbole
(édition 2000)
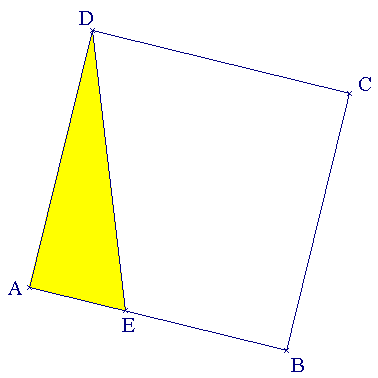
ABCD est un carré et E est un point du segment [AB] tel que EB = 6 cm
Quelle doit être la mesure du côté de ce carré pour que l'aire du carré
soit le triple de l'aire du triangle ADE ?
Ce problème semble facile pour des élèves de seconde. Le travail attendu est sur le choix de x,
soit AB = x, soit DE = x, puis sur l’écriture des équations correspondantes.
Petite inquiétude sur une découverte de la solution par intuition : AB = 18 cm
En fait le dessin représente une situation très éloignée de la solution, ce qui bloque, me semble-t-il la découverte de AB = 18.
Les élèves se répartissent en 3 catégories :
- un petit nombre a du mal à démarrer (choisir x puis comment calculer une aire…)
- Ceux qui choisissent AB = x ; l’équation obtenue est alors (x×(x-6)/2) 3 = x²
- Ceux qui choisissent DE = x ; l’équation obtenue est alors (x×(x+6)/2) 3 = (x + 6)²
Mais il est fréquent que les élèves trouvent une équation correcte, puis s’arrêtent (manque de confiance pour se lancer dans une aventure pareille !) ou font des erreurs de calcul.
La relance individuelle ou par petit groupe fait avancer. Beaucoup sont très content d’arriver ensuite à une solution correcte.
La synthèse finale au tableau avec les 2 équations est très enrichissante.
