Énoncé du problème
Niveau(x) concerné(s) : 3ème
(...après l'introduction des règles de calcul avec les racines
carrées ; en classe, seul puis à deux ou en groupe...)
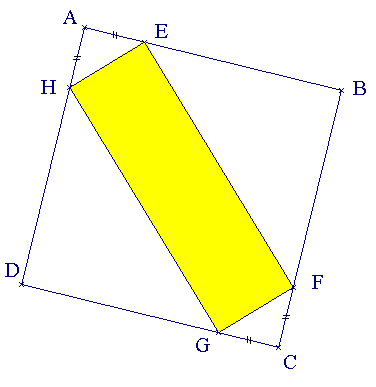
Sur le dessin ci-dessus :
|
Après le temps de travail personnel, faire une mise en commun sur la nature de EFGH : c’est un rectangle.
Les élèves risquent de se perdre dans des preuves complexes. Ce n’est pas l’objectif de l’exercice.
Une preuve simple : utilisation des angles de 45°…
Laisser ensuite chercher car l’introduction d’une lettre n’est pas automatique.
De plus ce qui est très riche est la diversité des méthodes :
Choisir AB = x
Choisir EB = x
Calculer directement avec le théorème de Pythagore la longueur EH ou FG en déduire EF puis EB…
Toutes les méthodes sont utilisées et la mise en commun est donc très riche.
EB = x
On obtient des équations équivalentes à :
(x + 2,4)² – x² – 2,4² = 30
Ensuite travail de développement, simplification…
d’où x = 6,25
le côté du carré est 8,65.
AB = x
On obtient des équations équivalentes à :
x² – 30 = 2,4² +(x – 2,4)²
Ensuite travail de développement, simplification…
on obtient x = 8,65
le côté du carré est 8,65.
Utilisation du théorème de Pythagore pour calculer EH.
Les élèves obtiennent EH² = 11,52 puis EH = sqrt 11,52 . Dans la correction on fait apparaître EH = 2,4 sqrt 2
Ils calculent EF = 30/sqrt11,52. Il faut alors calculer EB ou BF. C’est un bon exercice de réinvestissement, où le plus difficile est, pour l’élève, de s’engager dans le calcul.
Dans cette méthode l’élève a rarement posé EB = BF = x. Il obtient donc EB² + BF² = 900/11,52. Une aide au calcul avec radicaux est souvent nécessaire. Ensuite cela se passe assez bien car, 2 EB² = 78,125 puis EB² = 39,0625 et enfin EB = 6,25; le côté du carré est 8,65.
Dans la correction on peut utiliser EF = 30/(2,4×sqrt2) = 12,5/sqrt 2.
Puis l’équation 2 x² = (12,5/sqrt2)² soit 2 x² = 12,5²/2
puis x² = 12,5²/4 soit la solution positive x = 12,5/2 = 6,25
C’est un bon moment pour faire écrire dans le cours que la diagonale d’un carré de côté a mesure a
