Vers les équations
Pays: France
Niveau: (pas de niveau associé)
((pas de niveau associé))
Matière: Maths
Activité: Triangle et carré
C est un point de [AB]
ACDE est un carré
CFB est un triangle équilatéral
Où doit-on placer le point C pour que les périmètres du carré et du triangle soient égaux ?
Cas 1 : AB = 21 cm
Cas 2 : AB = 10 cm
Selon les variables choisies, la résolution ne met pas en œuvre les même compétences, le cas 1 peut être donné dès la 5ème
ACDE est un carré
CFB est un triangle équilatéral
Où doit-on placer le point C pour que les périmètres du carré et du triangle soient égaux ?
Cas 1 : AB = 21 cm
Cas 2 : AB = 10 cm
Selon les variables choisies, la résolution ne met pas en œuvre les même compétences, le cas 1 peut être donné dès la 5ème
Réactions d'élèves: Triangle et carré
1)Voici un exemple de résolution en 5ème :

l'élève fait plusieurs essais, puis réduit le nombre d'essais à faire en remarquant que le côté du triangle doit être plus grand que celui du carré. La solution étant entière, l'algèbre n'est pas nécessaire.

Toutefois certaines remarques intéressantes peuvent émerger, qui vont permettre de faire avancer vers une algébrisation :

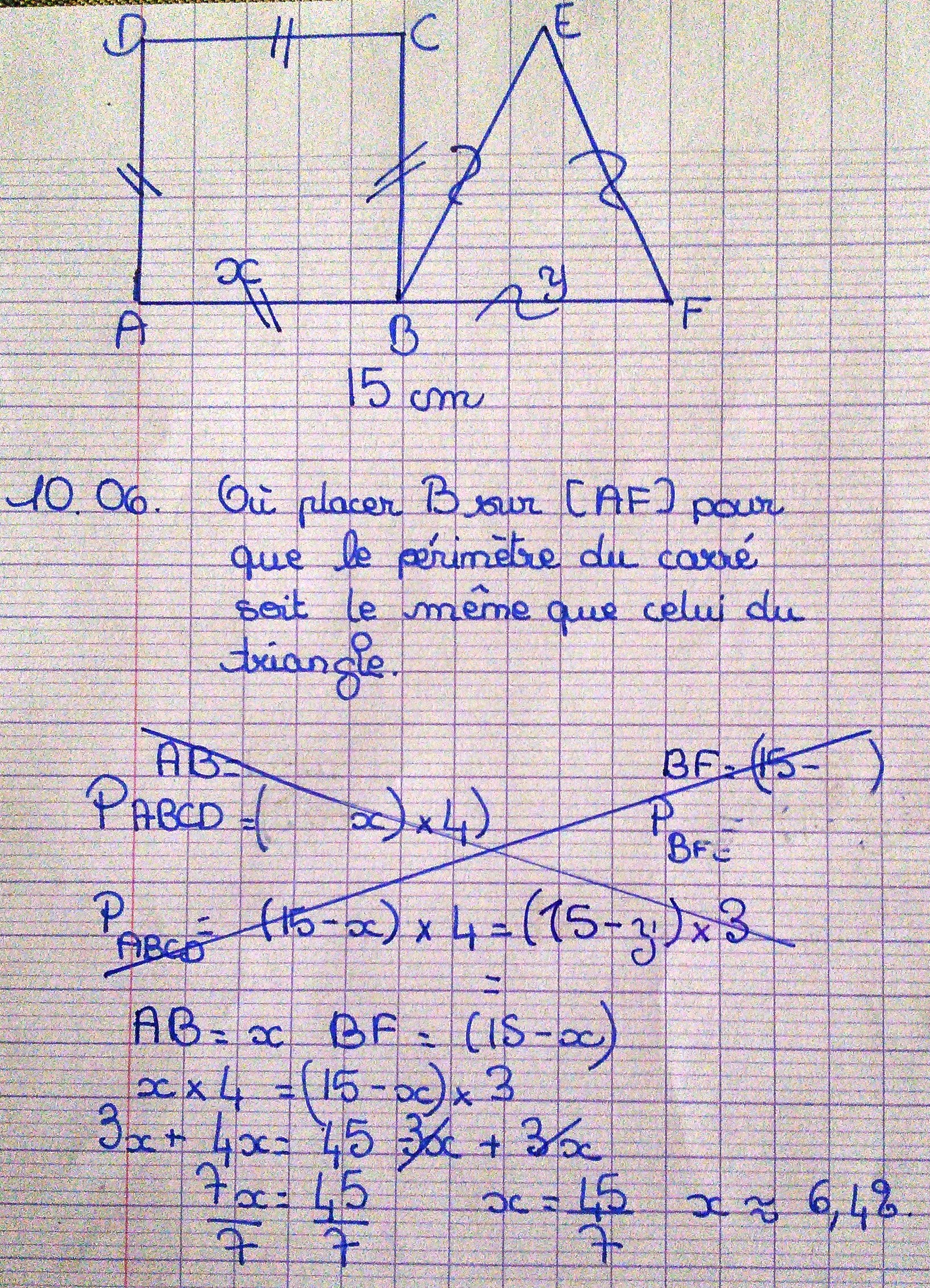


2) En 4ème et 3ème, les variables seront choisies pour encourager l'utilisation de la lettre. Les élèves cherchent dans un premier temps par essais erreur, puis face à la difficulté, réponse fractionnaire ou avec une précision au centième autre que le quart, tentent de mettre en équation.
Très souvent ils utilisent x et y pour les deux inconnues. Ici l'élève a ensuite dans un premier temps remplacé x par 15-y et y par 15-x

Cet autre élève a commencé par essayer de trouver par tâtonnement, pour finir avec une équation, la solution étant trop difficile à approcher.

Mise en oeuvre: Triangle et carré
Les problèmes de points mobiles peuvent se résoudre en
changeant de cadre. On traduit facilement la dépendance entre les deux
variables, ici la longueur du coté du carré et la longueur du coté du
triangle équilatéral, par une égalité. Le problème géométrique devient
donc un problème algébrique de résolution d'équation.
Cette activité trouvera toute sa place dans une progression de 4ème ou de 3ème. Néanmoins selon le choix qui sera fait pour la longueur du segment [AB], la méthode par essais erreur pourra être rapide et efficace (cas du choix de 21 qui donne un nombre entier comme solution de l'équation) ou difficile voire impossible (cas du choix de 10 qui donne une solution rationnelle) ce qui justifiera pleinement le passage à l'algèbre comme moyen plus performant pour trouver la solution.
Nous proposons cet exercice à nos élèves de 5ème en mise en train, dans la version AB = 21 cm (ou tout multiple de 7). Ils le résolvent arithmétiquement sans passage à l'algèbre. Lors de la mise en commun, ce sont les stratégies de recherche qui sont mise en avant et expliquées. L’intérêt de se servir de cet exercice en classe de 5ème est que lorsqu'ils le retrouveront avec d'autres variables didactiques, qui rendront nécessaire le passage à l'algèbre, le temps d'appropriation et de compréhension du problème sera moins long et ne viendra pas en sur-tache du problème réel.
Cette activité trouvera toute sa place dans une progression de 4ème ou de 3ème. Néanmoins selon le choix qui sera fait pour la longueur du segment [AB], la méthode par essais erreur pourra être rapide et efficace (cas du choix de 21 qui donne un nombre entier comme solution de l'équation) ou difficile voire impossible (cas du choix de 10 qui donne une solution rationnelle) ce qui justifiera pleinement le passage à l'algèbre comme moyen plus performant pour trouver la solution.
Nous proposons cet exercice à nos élèves de 5ème en mise en train, dans la version AB = 21 cm (ou tout multiple de 7). Ils le résolvent arithmétiquement sans passage à l'algèbre. Lors de la mise en commun, ce sont les stratégies de recherche qui sont mise en avant et expliquées. L’intérêt de se servir de cet exercice en classe de 5ème est que lorsqu'ils le retrouveront avec d'autres variables didactiques, qui rendront nécessaire le passage à l'algèbre, le temps d'appropriation et de compréhension du problème sera moins long et ne viendra pas en sur-tache du problème réel.
But: Triangle et carré
Principe 2 : Ne pas indiquer de principe de résolution (en particulier l'utilisation de la lettre)
Principe 3 : Favoriser les changements de registre
Principe 3 : Favoriser les changements de registre
