Énoncé du problème
Niveau(x) concerné(s) : 3ème (possible en devoir surveillé)
(...après l'introduction des règles de calcul avec les racines
carrées ; en classe, seul puis à deux ou en groupe...)
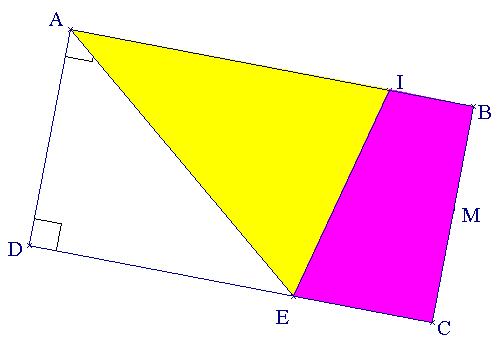
ABCD est un rectangle tel que :
- AD = 12 cm et AB = 18 cm
- CE = 8,25 cm
Trouver la longueur BI pour que l'aire du triangle AIE soit égale à l'aire du trapèze rectangle IBCE.
(donner la formule de calcul de l'aire d'un trapèze en rappel)
La diversité des méthodes va permettre à presque tous les élèves de démarrer cet exercice.
Même s’ils ne terminent pas une partie de la note prévue sera attribuée pour la démarche.
Méthodes :
- Choisir IB = x
- Choisir AI = x
Calculer l’aire du rectangle puis celle du triangle ADE et par soustraction on obtient le double de l’aire du triangle AIE ou de l’aire du trapèze IBCE.
La solution, BI = 4,875 n’est pas directement accessible.
La méthode avec IB = x est majoritaire, on ne trouve pas dans mon devoir AI = x.
La difficulté principale, pour démarrer, est de penser qu’une hauteur du triangle AIE est CB ou AB dont la mesure est donnée (12 cm).
La deuxième difficulté est d’arriver à se débrouiller avec une équation du type :
[(18 – x) ×12]/2 = (8,25 + x) 12 1/2. Mais à ce niveau on a déjà la moitié des points !
La méthode , calcul de l’aire de ADE…, est assez fréquente et bien appréciée à la correction par les élèves plus faibles.
