Techniques de calculs

Pays: France

Niveau: (pas de niveau associé) ((pas de niveau associé))

Matière: Maths

Activité: Le poisson

Calculer le périmètre de ce dessin pour les valeurs de a suivantes :

a = 2 a = 3 a = 1/2 a = 1/10 a = 8 a = 10

Trouver une méthode qui permet d'aller le plus vite possible pour faire tous ces calculs.
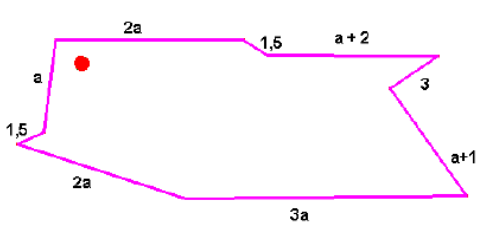
Vous avez 5 minutes.

Prolongements

On peut prolonger par des questions qui amènent à une résolution d'équations :

• le périmètre est 659, quel était le nombre de départ ?

Synthèse: Le poisson

Il s'agit ici de rappeler les règles du calcul algébrique.

But: Le poisson

But de cette activité

Montrer l'intérêt et la nécessité, de trouver une formule plus simple qui permet de calculer rapidement (justification des règles de calcul algébrique). (principe 5)

Favoriser les justifications des calculs par l'utilisation de règles algébriques.(principe 7)

Travailler sur les vérifications.(principe 4)

Mise en oeuvre: Le poisson

Les élèves travaillent par groupes de 2 ou 3. Ils peuvent utiliser leur calculatrice. Le professeur passe auprès d'eux pour leur rappeler la contrainte de temps.
Comme pour la première activité, la mise en commun est ensuite faite au tableau pour :
• Trouver les différents résultats.
• Déterminer la méthode qui permet de faire les calculs rapidement, c'est-à-dire la formule 10 x + 9
• Faire fonctionner cette formule sur d'autres nombres.

Réactions d'élèves: Le poisson

Analyse de cette activité
L'objectif principal est de montrer aux élèves qu'on peut faire des calculs avec des expressions algébriques. D'autres objectifs sont de faire faire des calculs simples et de réutiliser des expressions tels que 3x. Pour le moment nous avons choisi de partir d'une situation très modélisée puisque les longueurs des segments comportent déjà des expressions algébriques. Nous avons volontairement choisi d'arriver à une expression très simple 10x + 9 pour montrer la rapidité de calcul. Le choix de la contrainte de temps est très important car sinon les élèves font les calculs les uns à la suite des autres avec leur calculatrice. Il faut également donner un nombre important de calcul avec des valeurs de x non entières.

Les expressions /formules produites
La plupart des élèves pensent à ajouter les valeurs numériques, ils ont donc des expressions comme 9 + x + 2x + 3x + x + 2x + x. D'autres élèves vont également ajouter les x dont le coefficient est 1 donc 9 + 3x + 2x + 3x + 2x. La façon dont les élèves parcourent le poisson (soit en commençant par la droite ou la gauche) va influer sur le résultat.