Dans cette partie, nous commençons
à introduire des types de problèmes classiques sur les
preuves en algèbre. Nous proposons tout d'abord des programmes
de calcul dont le résultat (remarquable) peut être
prouvé grâce à une réduction.
Je choisis le nombre 3, je lui ajoute 4, je multiplie le résultat par 5 puis je retranche 20.Calculer le résultat obtenu. Faire de même avec 6, 8, 48. Que remarquez vous ?
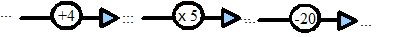
Le programme renvoie 5 fois le nombre
choisi au départ, les élèves peuvent remarquer
ce résultat particulier (éventuellement dès la
6ème en justifiant par le fait que l'on ajoute 4x5 puis que
l'on soustrait 20) et le prouver grâce à la
distributivité.
Pour les niveaux 4ème et 3ème,
la preuve pourra faire appel à la double distributivité
ou aux identités remarquables pour factoriser.
Nous proposons ensuite aux élèves
de créer leurs propres programmes que leurs camarades devront
découvrir en le faisant fonctionner plusieurs fois. Ils seront
donc amenés à mettre en œuvre des stratégies
de recherche : les nombres ne sont plus choisis au hasard :
importance du 0, recherche d'une proportionnalité ou d'une
proportionnalité décalée (fonction affine)...
L'élève responsable
fabrique son programme de calcul.
Par exemple 3 donne 7.
Ensuite ses camarades proposent des nombres avec lesquels le faire fonctionner :
- par exemple 2, espérant trouver 2 x 2 + 1 = 5
- ou 9, espérant trouver 9 x 7/3 = 21
- ou encore 1, espérant trouver 1 + 4 = 5
